Lineær Regresjon. Digital samling 1

Njål Foldnes

Et lite eksempel for enkel regresjon

Lekeeksempel

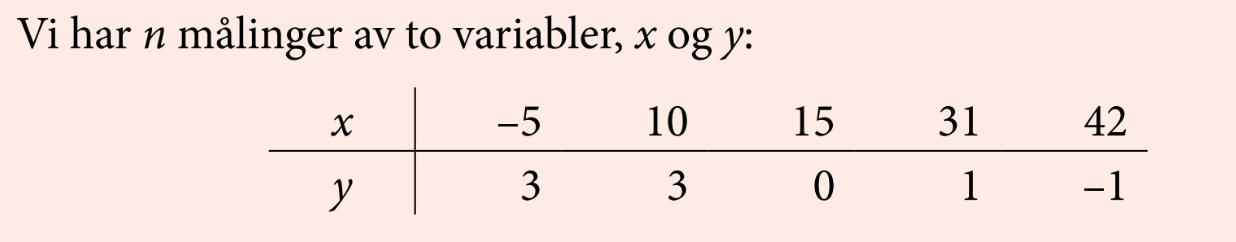
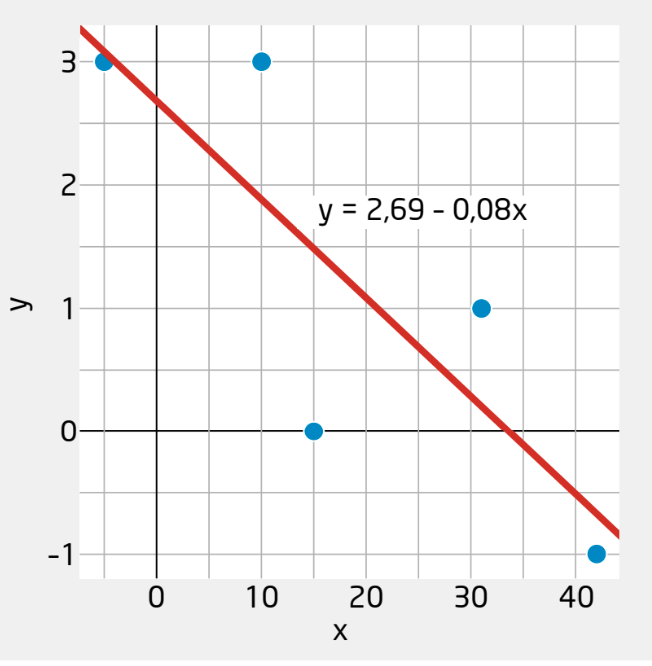
Estimere modellen med \(\textsf{lm()}\) og plotte

x <- c(-5, 10, 15, 31, 42)
y <- c(3,3,0,1, -1)
model <- lm(y~x)
qplot(x,y)+geom_smooth(method="lm", se=F)

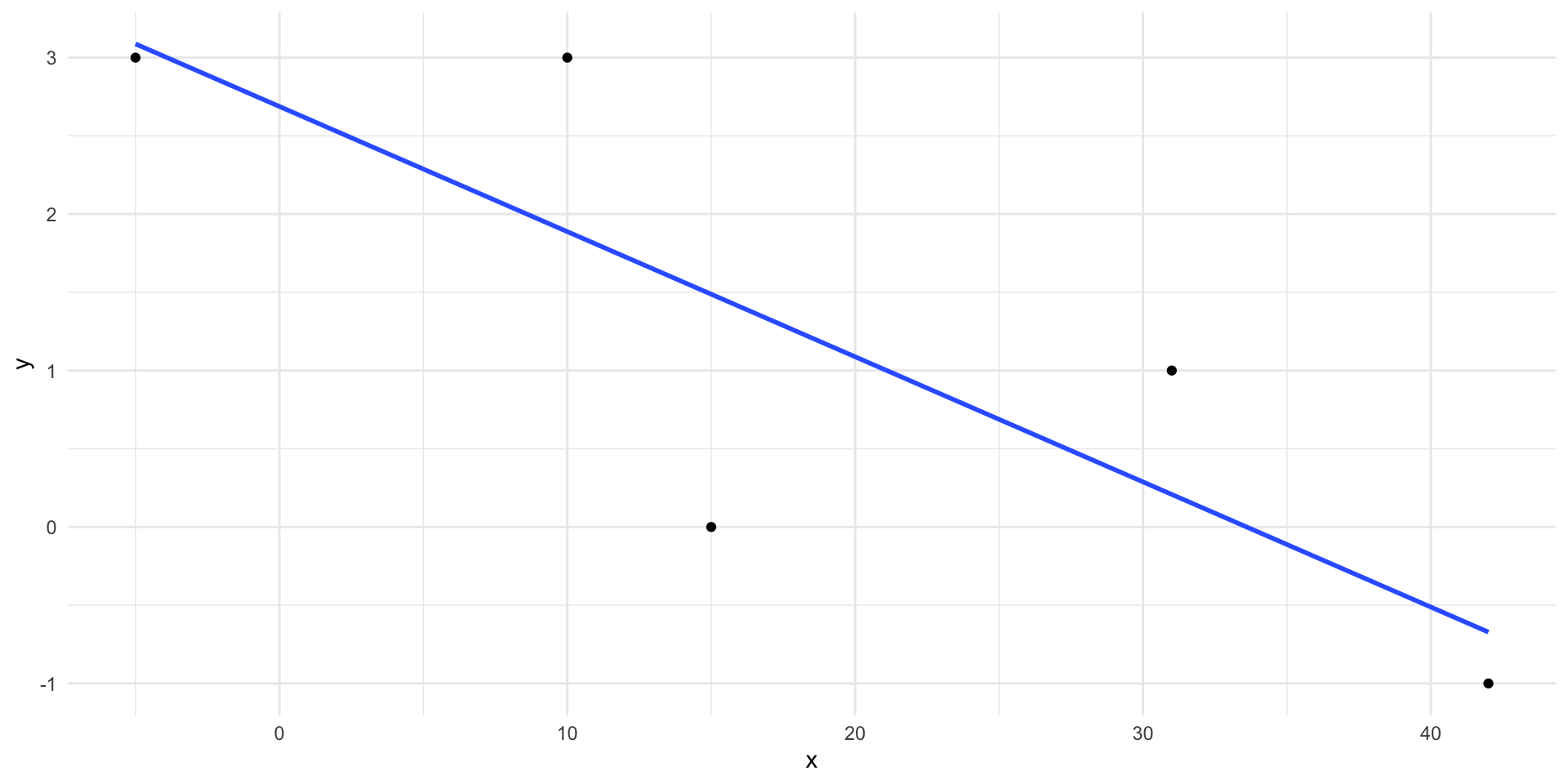
Utskrift fra \(\textsf{lm()}\)

summary(model)

Call:
lm(formula = y ~ x)

Residuals:
       1        2        3        4        5 
-0.08772  1.11210 -1.48796  0.79185 -0.32828 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  2.68778    0.79939   3.362   0.0437 *
x           -0.07999    0.03223  -2.481   0.0892 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.182 on 3 degrees of freedom
Multiple R-squared:  0.6724,    Adjusted R-squared:  0.5632 
F-statistic: 6.158 on 1 and 3 DF,  p-value: 0.08916

\(R^2\): forklart varians

  • Residualet: Avstand fra den faktiske \(y\) verdien til den \(y\) som modellen predikerer (på linja)

  • \(R^2\): Andel av variasjonen i \(y\) som kan forklares av \(x\) (to versjoner). Jo høyere, jo bedre er linja som forklaringsmodell

Predikere nye verdier

Dersom vi har en ny verdie, \(x=20\) kan vi bruke linja til en kvalifisert gjetning på hva \(y\) vil være:

yhat <- predict(model, newdata=data.frame(x=20))
yhat
       1 
1.088017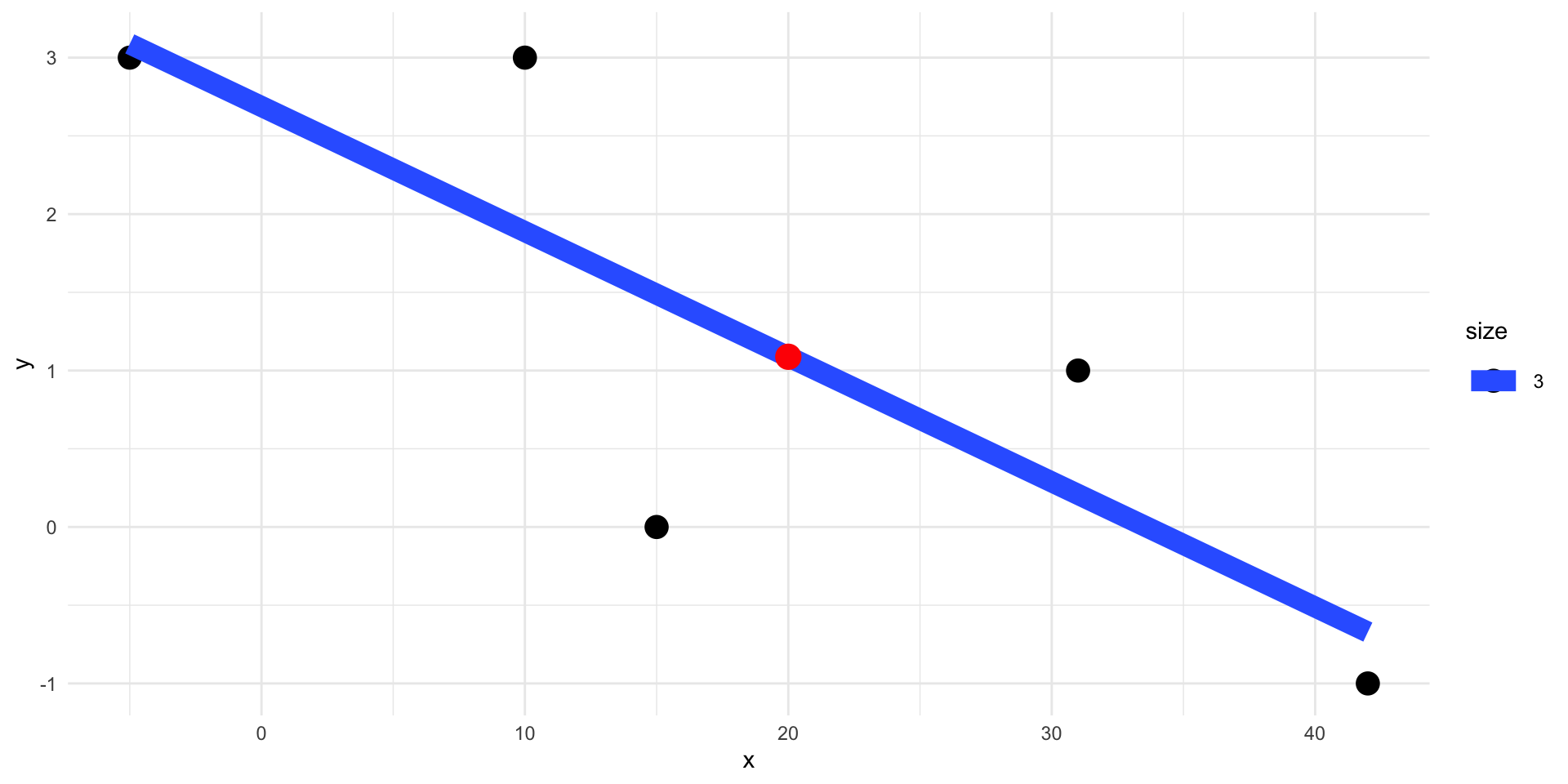 
qplot(x,y, size=3)+geom_smooth(method="lm", se=F)+geom_point(aes(x=20, y=yhat),size=5, color="red")

Enkel regresjon

Vi ønsker å studere en kontinuerlig variabel \(y\). Denne kalles den avhengige variabelen.

Vi forklarer variasjonen i \(y\) ved hjelp av en enkel forklaringsvariabel \(x\) og en lineær sammenheng

\[ y = \beta_0+ \beta_1 x + \epsilon\]

  • \(\beta_1 > 0\): positiv sammenheng mellom \(x\) og \(y\)
  • \(\beta_1 < 0\): negativ sammenheng mellom \(x\) og \(y\)
  • \(\beta_1 = 0\): ingen sammenheng mellom \(x\) og \(y\)

Antagelser i lineær regresjon

  • Linearitet!
  • Homoskedastisitet: Residualene må ha samme varians uansett hva \(x\) er. Kan sjekkes med å plotte residualene vs de predikerte (fitted values)
  • Hvis det er et lite utvalg så bør residualene være normalfordelte

OK: lineært og homoskedastisk

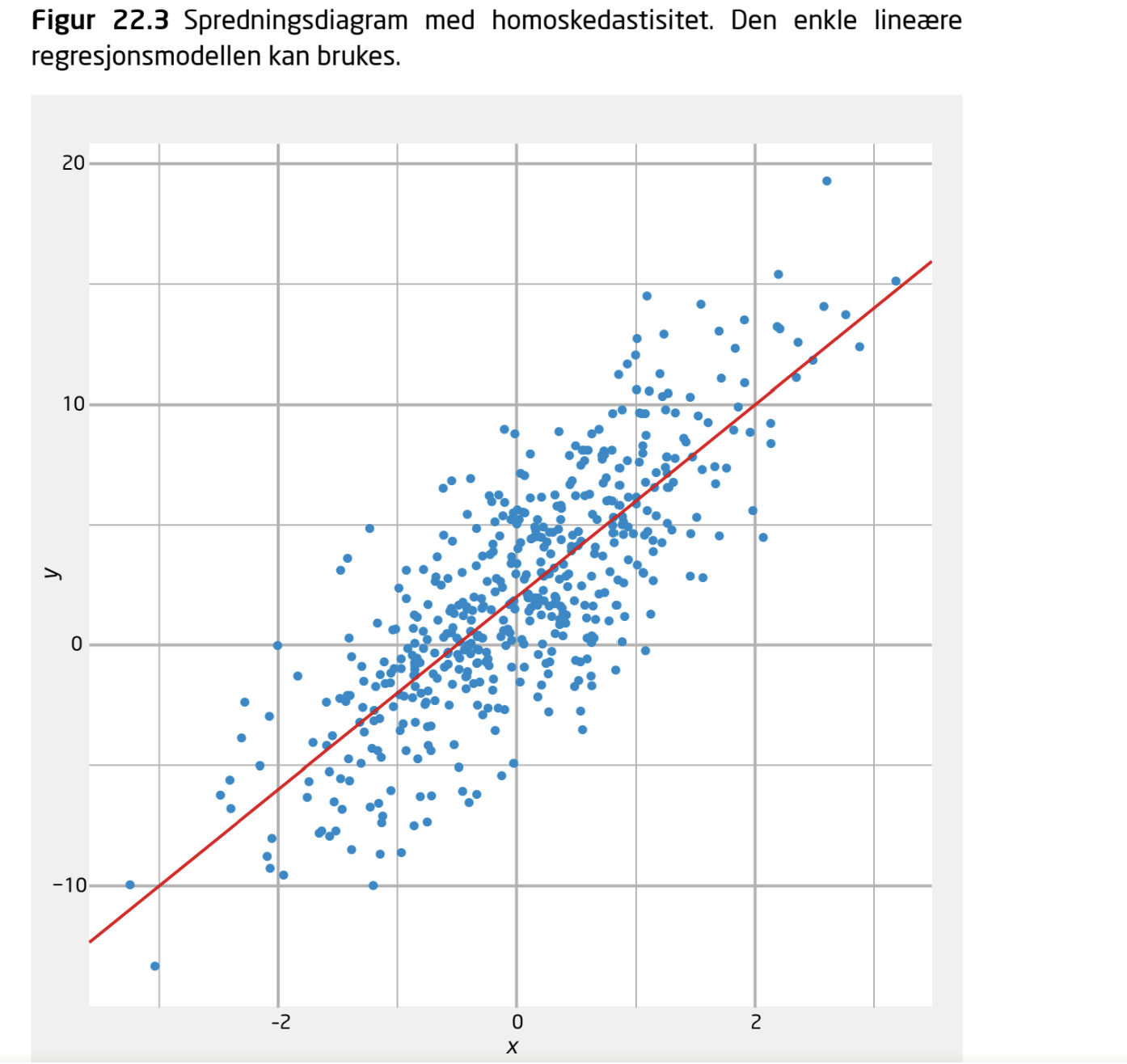
Perfekt

IKKE OK: ikke lineært!

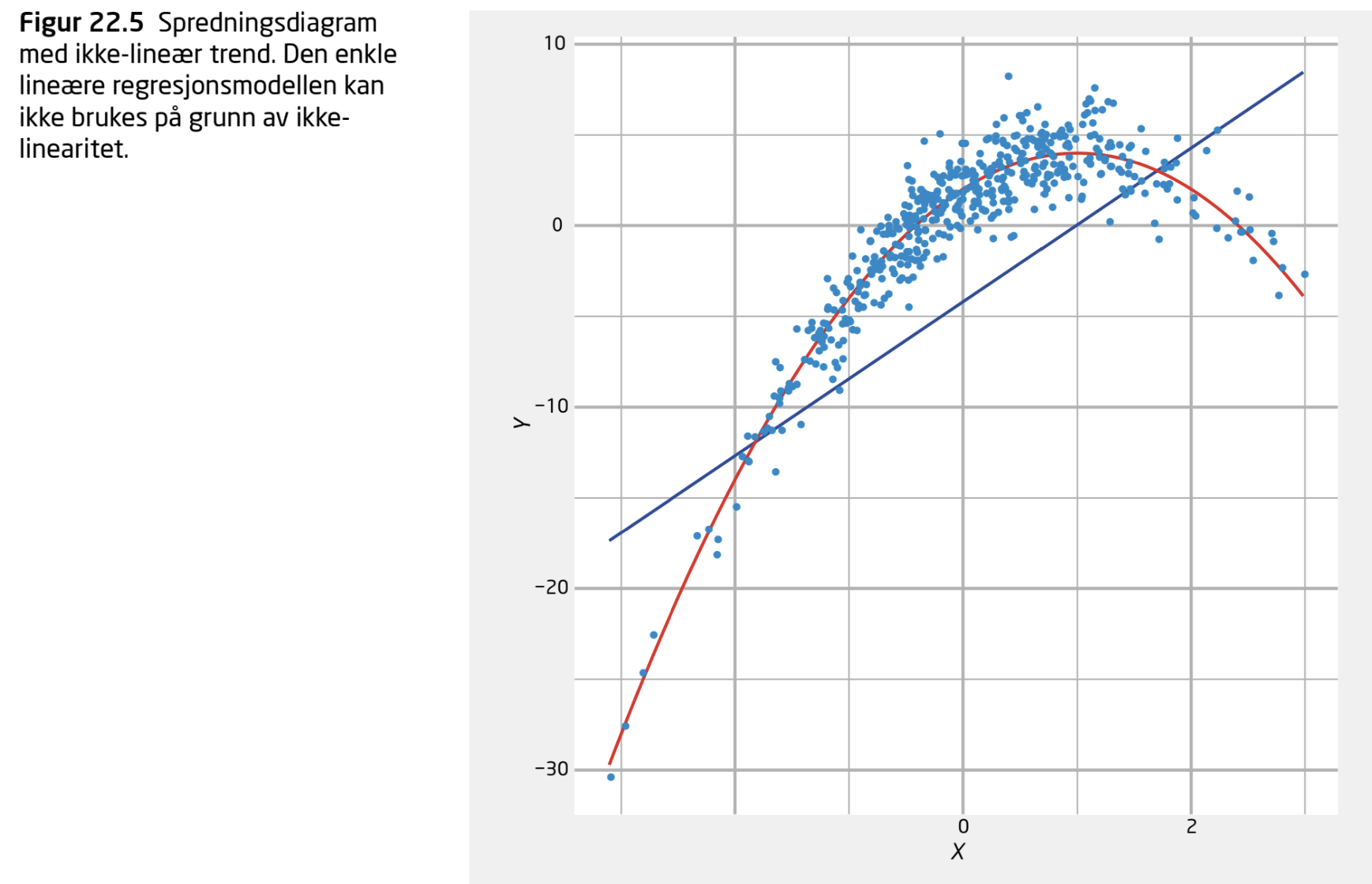
Sammenhengen er ikke lineær

Kan fikses ved å ta med \(x^2\) som uavhengig variabel

IKKE OK: homoskedastiske feilledd

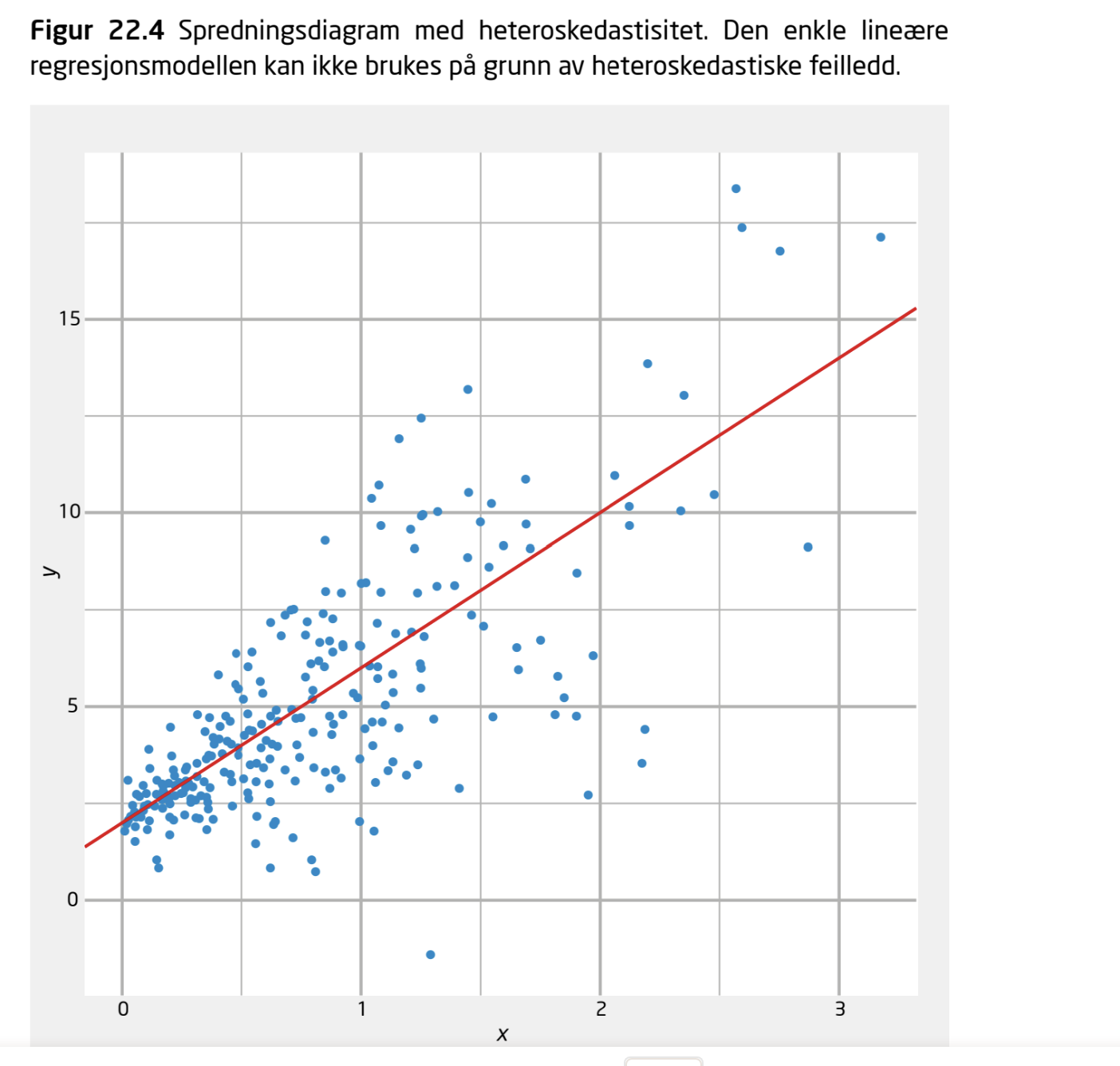
Residualene varierer mer jo større \(x\) er

Kan fikses ved å bruke en robust estimator av White-typen

Reelt datasett: Trivsel og mobilbruk blant engelske 15 åringer

Trivsel og sosiale medier engelske 15 åringer

Przybylski, A. & Weinstein, N. (2017). A Large-Scale Test of the Goldilocks Hypothesis. Psychological Science, 28, 204–215.

Storskala studie som finner støtte til “Goldilocks” hypotesen.

Dataene er tilgjengelige her

Trivsel - Wellbeing

Vi ønsker å studere trivsel. Det er vår avhengige variabel:

Trivsel målt med Warwick-Edinburgh Mental Well-Being Scale (WEMWBS). Spørreskjema med 14 items og 5 responsnivå. Vi bruker summescoren

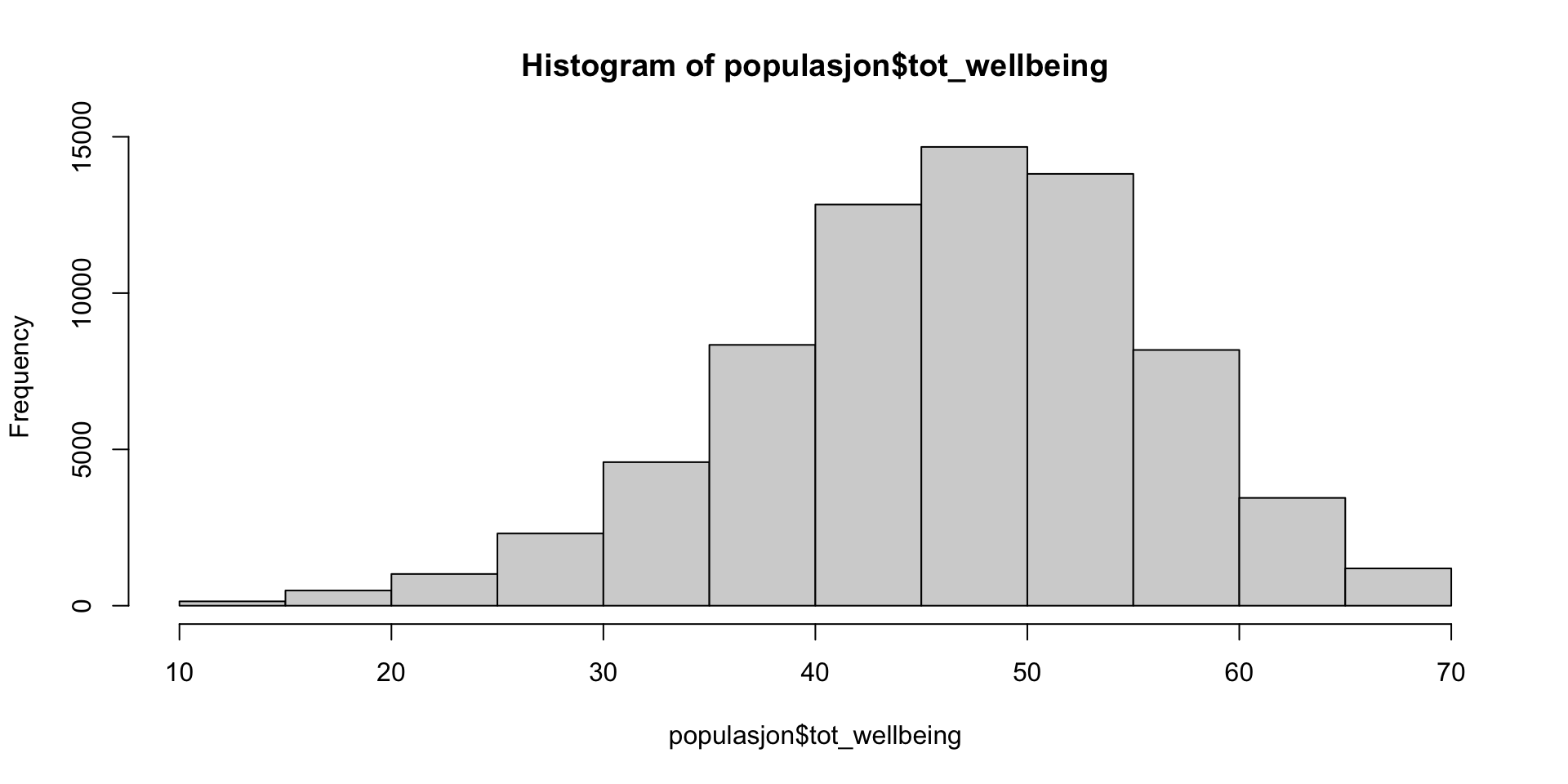
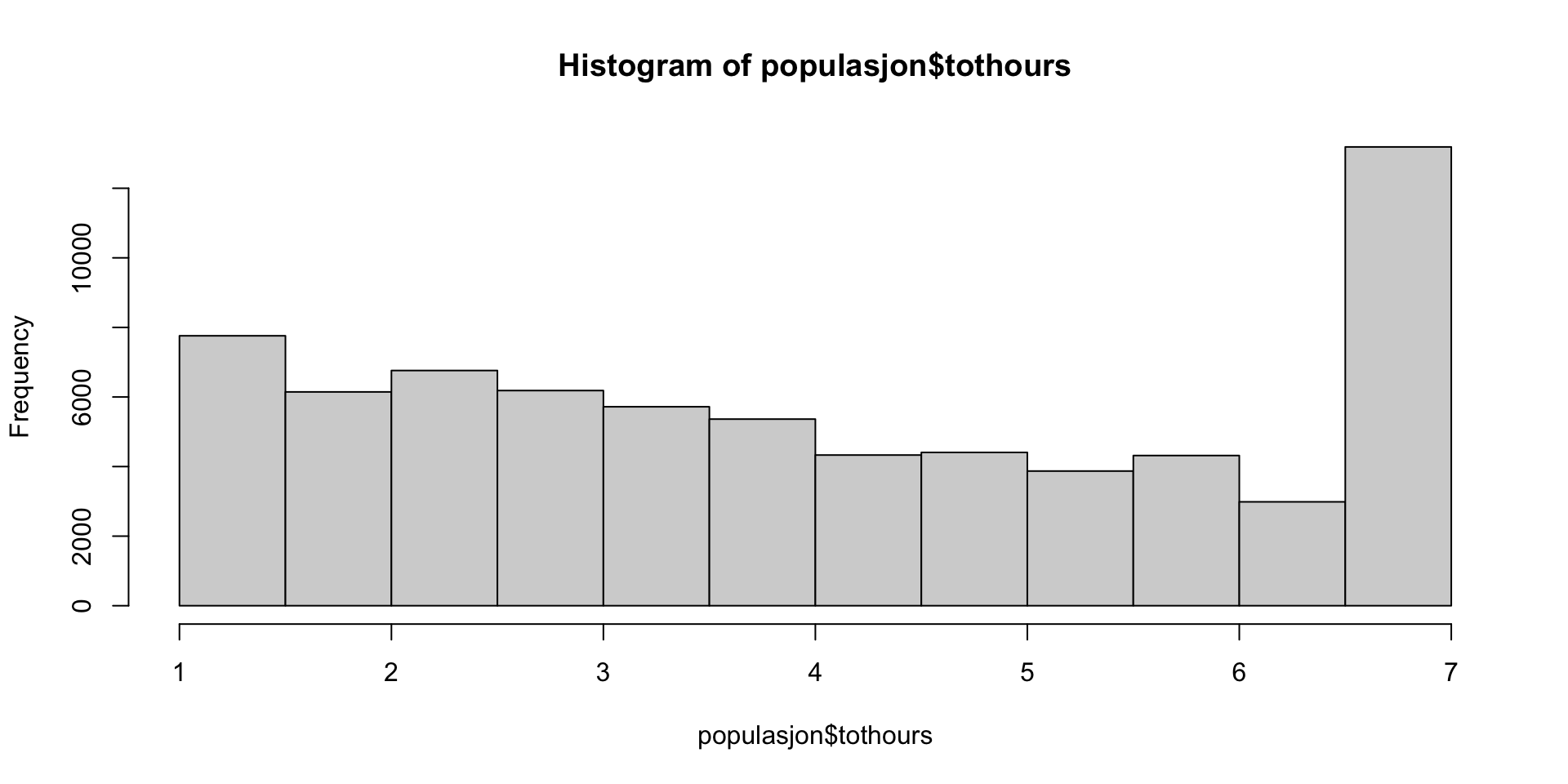
Vi har 71033 deltagere! La oss tenke på dette som POPULASJONEN

Negativ trivsel og telefonbruk i “populasjonen”

popmodel <- lm(tot_wellbeing~ tothours, data=populasjon)
popmodel %>% tidy() %>% kable(digits=2)
term estimate std.error statistic p.value
(Intercept) 50.31 0.09 585.03 0
tothours -0.81 0.02 -43.99 0

En time ekstra daglig mobilbruk gir en forventet nedgang i trivsel på 0.81

Sammenheng trivsel og telefonbruk i et tilfeldig utvalg av 400 15-åringer

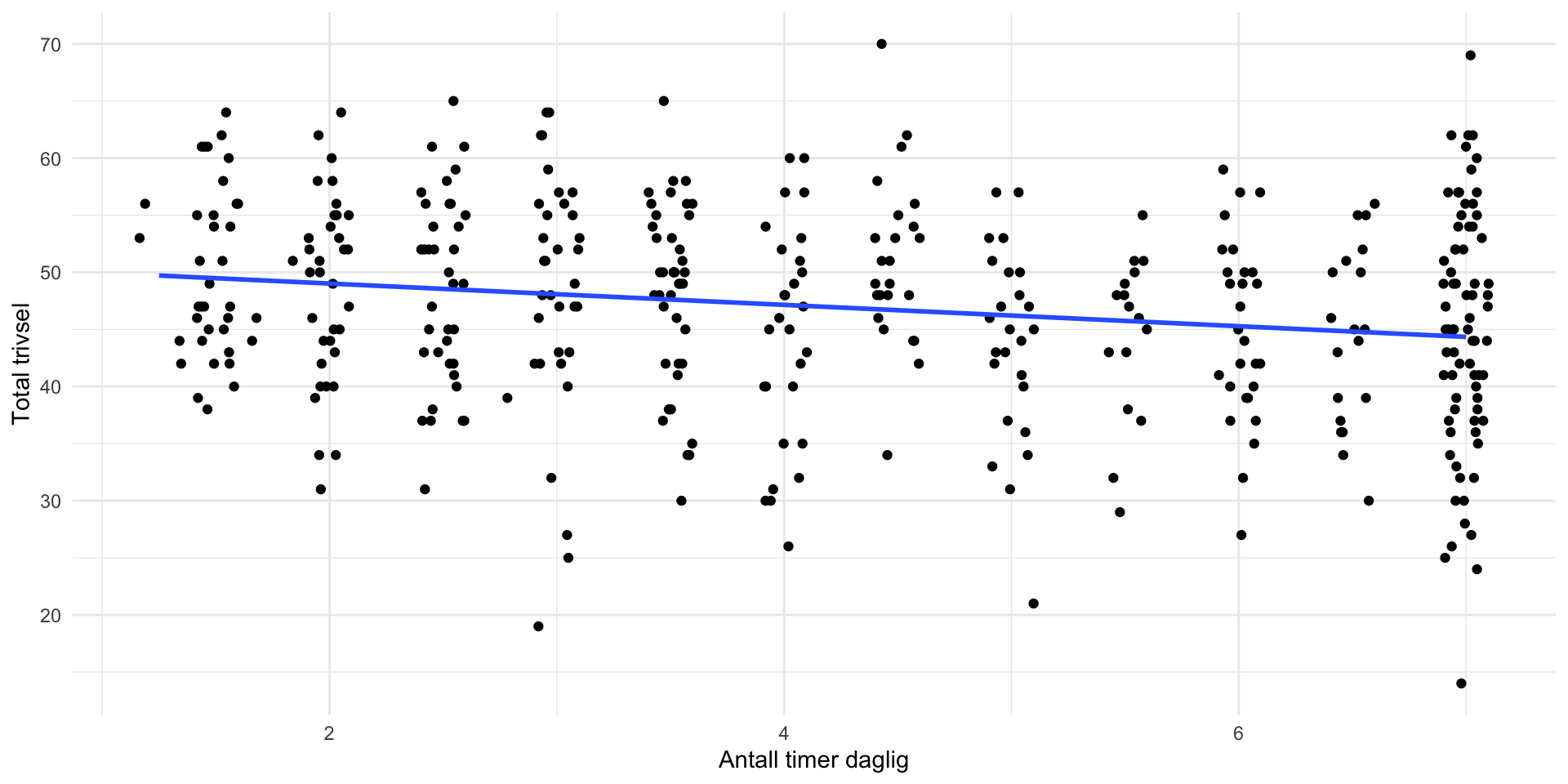
Regresjon i utvalget

term estimate std.error statistic p.value
(Intercept) 50.89 1.09 46.55 0
tothours -0.93 0.23 -4.01 0

Ganske likt populasjonsverdiene! Vi har linearitet.

Homoskedastiske feilledd?

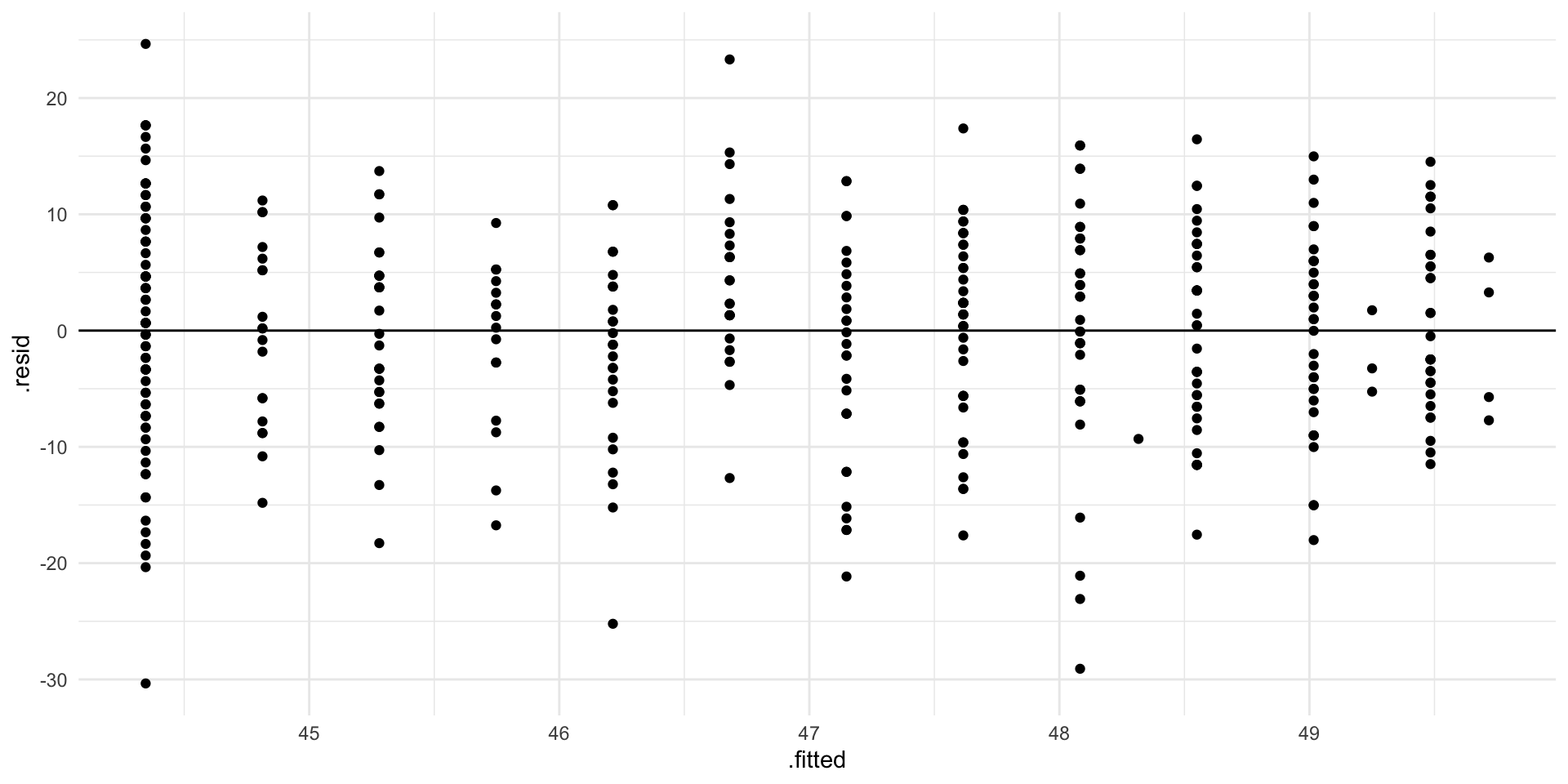
Her har vi tilnærmet homoskedastisitet!

Husk at estimatene er usikre!

Her er fire andre utvalg av størrelse \(n=400\). Vi ser at intercept og slope varierer endel!

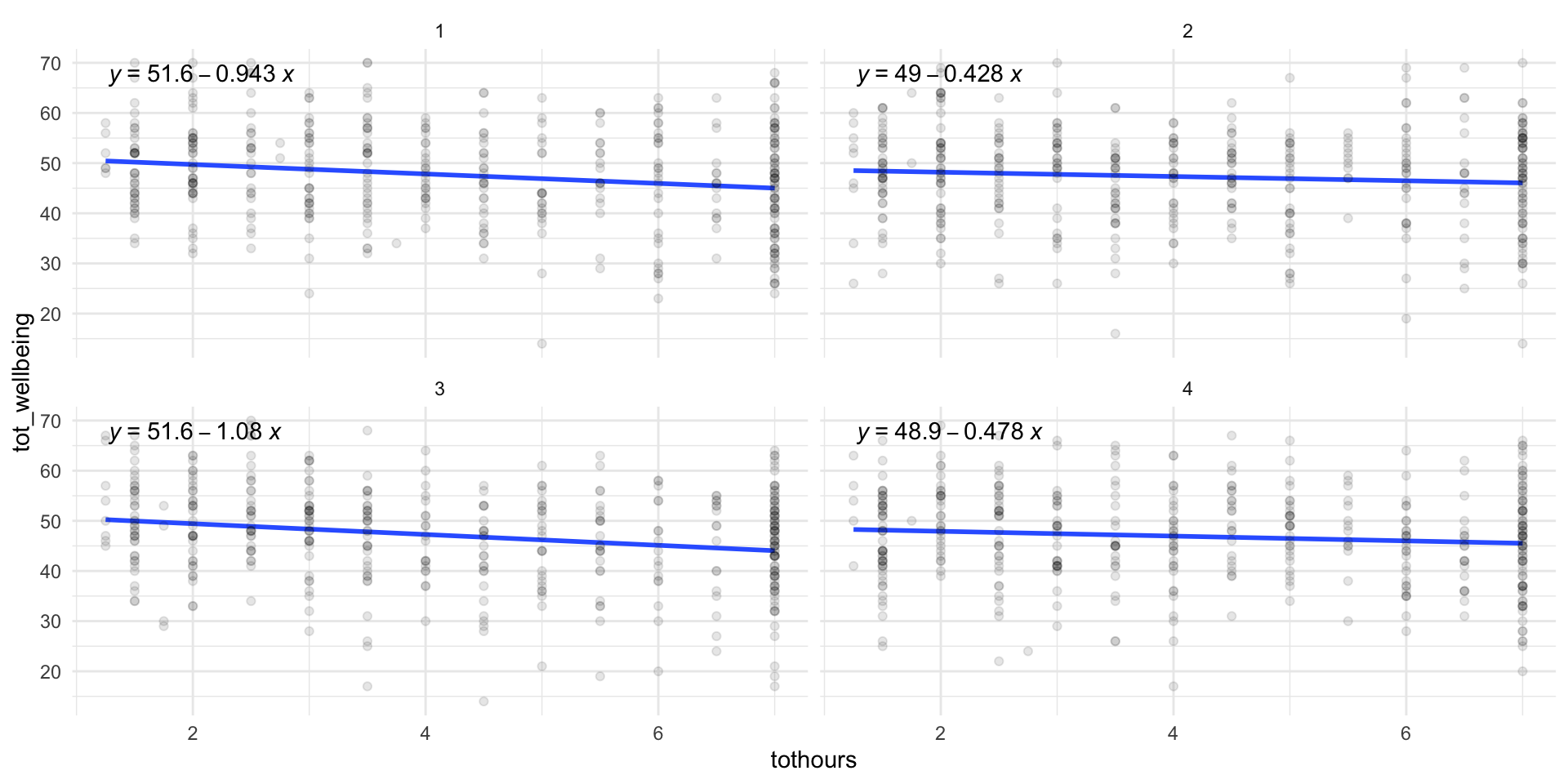
Multippel regresjon

Multippel regresjon

En enkel uvidelse av enkel regresjon, der vi har flere uavhengige variable

\[ y = \beta_0+ \beta_1 x_1 + \beta_2 x_2+ \beta_3 x_3+ \epsilon\] Her har vi TRE forklaringsvariabler \(x_1,x_2, x_3\) som forklarer hvorfor \(y\) varierer!

Ceteris paribus

Ceteris paribus [keːˈtɛ.riːsˈpa.rɪ.bʊs] latinsk for “alt annet likt”

I multippel regresjon får vi effekten av en variabel på \(y\), “alt annet likt”. Vi kontrollerer for de andre variablene!

For eksempel: \[ y = 1+ 2 \cdot x_1 - x_2+ 0.5 \cdot x_3+ \epsilon\] Når \(x_1\) øker med 1 enhet, så øker \(y\) med 2 enheter, alt annet likt. Dvs at vi holder \(x_2\) og \(x_3\) fast, og får isolert sammenhengen mellom \(x_1\) og \(y\).

Eksempel: Effekt av telefonbruk på Well-being, kontrollert for kjønn

Gutter har høyere trivsel (6.5 poeng) og lavere mobilforbruk:

utvalg %>% group_by(male) %>%
  summarise(wbsnitt=mean(tot_wellbeing),
            tothoursnitt=mean(tothours))
# A tibble: 2 × 3
  male  wbsnitt tothoursnitt
  <fct>   <dbl>        <dbl>
1 0        44.5         4.52
2 1        51.0         3.89

Vi tar med kjønn som forklaringsvariabel. Dette er en kategorisk variabel, vi koder den med en dummy variabel: male=0 betyr jente, male=1 betyr gutt.

Kategoriske variabler og dummy-koding

kategoriske variabler kan kodes med dummyvariabler i regresjon. Dersom vi har \(K\) kategorier, trenger vi \(K-1\) dummy variabler:

  • Kjønn: \(K=2\). Vi har \(K-1=2-1=1\) dummy variabel.
  • USA politisk tilørighet: Dem, Rep, Ind: \(K=3\). Vi har \(K-1=2-1=2\) dummy variabler. For eksempel kan vi har \(R=1\) hvis republikaner, og \(D=1\) hvis demokrat. Vi trenger ikke \(Ind\), siden dersom \(R=0\) og \(D=0\) så vet vi at det er en independent velger.

Multippel regresjon i R

\[ \text{tot_wellbeing} = \beta_0+ \beta_1 \cdot \text{tothours}+ \beta_2 \cdot \text{male}+\epsilon\]

multmodel <- lm(tot_wellbeing~ tothours+male, data=utvalg)
multmodel %>% tidy() %>% kable(digits=2)
term estimate std.error statistic p.value
(Intercept) 47.57 1.14 41.74 0
tothours -0.69 0.22 -3.08 0
male1 6.07 0.88 6.92 0

Telefonbruk, kjønn og well-being

term estimate std.error statistic p.value
(Intercept) 47.57 1.14 41.74 0
tothours -0.69 0.22 -3.08 0
male1 6.07 0.88 6.92 0

Effekten av telefonbruk er litt mindre når vi kontrollerer for kjønn (-0.934 \(\rightarrow\) -0.688 )

Og effekt av kjønn på trivsel, når vi kontrollerer for telefonbruk, er lavere nå, 6.07. Så noe av den observerte trivselforskjellen på 6.5 kan forklares ved at guttene er mindre på mobil, og at mobil ikke er bra for wellbeing!

ANOVA

ANOVA analysis of variance

I intro statistikk så lærer man anova. - Du har flere grupper i populasjonen - Du lurer på om \(y\) har samme gjennomsnitt i alle gruppene - \(H_0:\mu_1=\mu_2=\cdots=\mu_g\) - Alternativhypotesen er at gruppegjennomsnittene ikke alle er like!

Eksempel

Vi antar at i utvalget var det 4 skoler. Vi ønsker å teste om well-being er den samme på alle skolene:

aov(tot_wellbeing~ school, utvalg) %>% tidy() %>% kable(digits=2)
term df sumsq meansq statistic p.value
school 3 92.19 30.73 0.38 0.77
Residuals 396 32388.05 81.79 NA NA

Vi har ikke støtte for å hevde at det er forskjell i well-being mellom de 4 skolene (p-verdi=.77 vi beholder \(H_0\))

hjem