Quiz 19.mars

  1. Forklar hvorfor publikasjonsbias kan være en av årsakene til replikasjonskrisen.

Svar: Det er vanskelig å replikere en studie som er en falsk positiv. Falske positive er overrepresentert i den publiserte litteraturen, grunnet publikasjonsbias.

  1. Hva regnes som en stor effektstørrelse for Cohens \(d\)?

Svar: I mange felt er \(d\) større ennn .5 regnet som stor.

  1. Cohen \(d=0.2\) for en intervensjon, tolk dette tallet i en setning som inneholder ordene “standardavvik” og “økning i gjennomsnittsscore”.

  2. En mindfulness-intervensjon gjør at konsentrasjonen i intervensjonsgruppa er 3 poeng høyere enn i kontrollgrupa. Hvis den poolede standardavviket \(s_p\) er 10 poeng, hva er da effektstørrelsen?

  3. Vi genererer et datasett som måler konsentrasjon på en skala 1-20 etter en mindfulness-intervensjon:

library(tidyverse)
set.seed(1)
gruppe <- sample(c("I","K"), size=100,replace=T)
konsentrasjon <- 10+as.numeric(gruppe=="I")+runif(length(gruppe), -6,6) %>% round(0)
minedata <- data.frame(gruppe, konsentrasjon)

Hvor mange deltagere var i kontroll og i intervensjonsgruppa? Hint:

table(gruppe)
gruppe
 I  K 
49 51
  1. Lag et histogram over konsentrasjon
hist(minedata$konsentrasjon)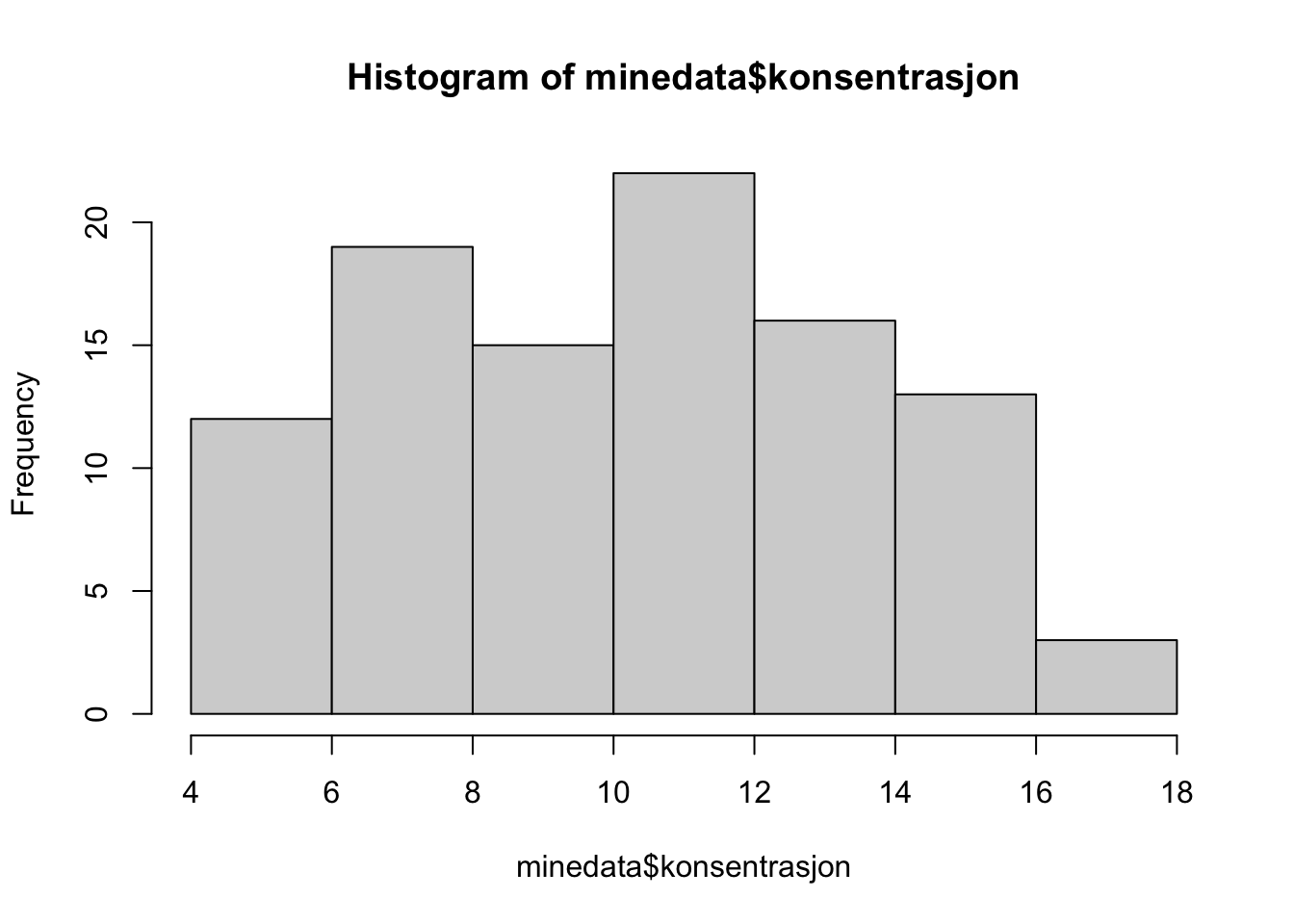

  1. Hva er max verdi av konsentrasjon?

  2. Lag et boksplot over konsentrasjon og bruk det til å anslå interkvartilbredden.

boxplot(minedata$konsentrasjon)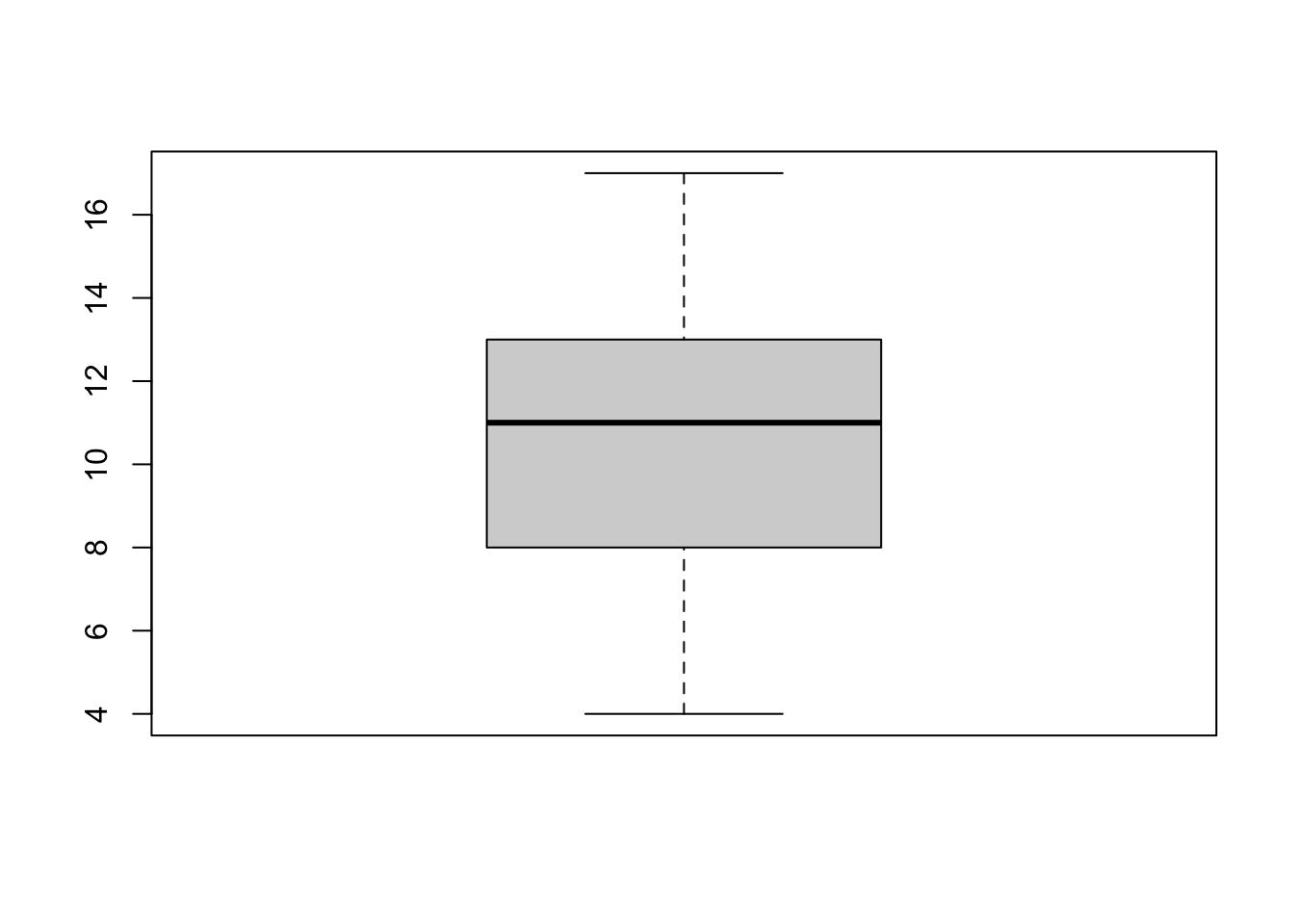

  1. Hva er standardavviket til konsentrasjon?

  2. Er det forskjell i konsentrasjon i de to gruppene? Bruk en t-test

t.test(konsentrasjon~gruppe, data=minedata)

  1. Hva var differansen i gjennomsnitt?

  2. Beregn cohens d for effektstørrelsen av intervensjonen.

library(psych)
cohen.d(konsentrasjon~gruppe, data=minedata)
Call: cohen.d(x = konsentrasjon ~ gruppe, data = minedata)
Cohen d statistic of difference between two means
              lower effect upper
konsentrasjon -0.64  -0.25  0.14

Multivariate (Mahalanobis) distance between groups
[1] 0.25
r equivalent of difference between two means
konsentrasjon 
        -0.12

  1. Hva er konfidensintervallet for \(d\). Gi en tolkning av det faktum at det ikke inneholder \(0\).

  2. Vi Lager et nytt simulert datasett for effekt av konsentrasjon på eksamensresultat:

set.seed(1)
poeng <- 25+2*konsentrasjon+rnorm(length(konsentrasjon), mean=0, sd=10)
eksamendata <- data.frame(poeng, konsentrasjon)
  1. Plott konsentrasjon mot eksamensresultat og beregn korrelasjonen
plot(eksamendata$konsentrasjon, eksamendata$poeng)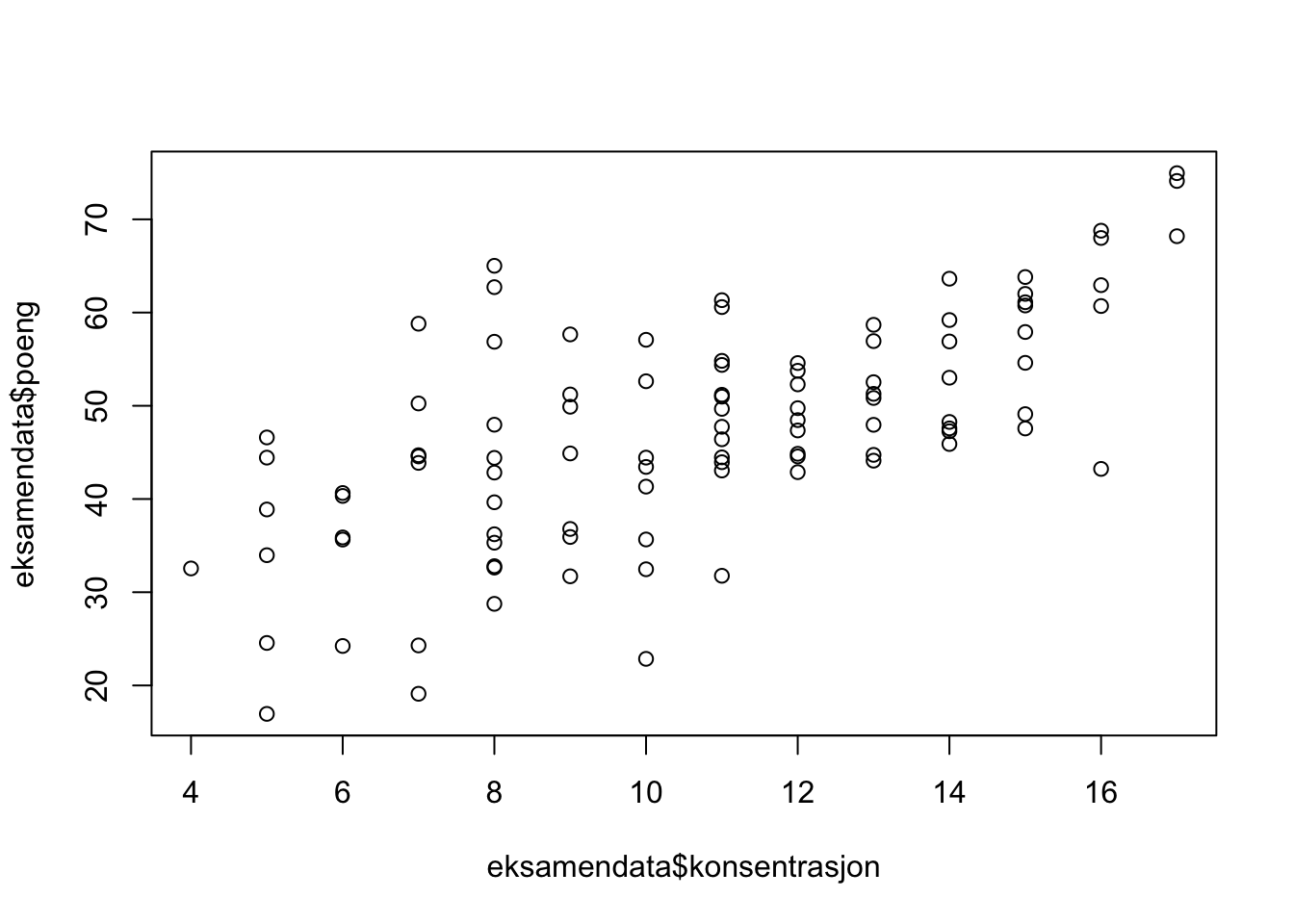

  1. Estimer regresjonsmodellen \(Poeng=\beta_0+ \beta_1 konsentrasjon + \epsilon\) og tolk stigningstallet \(\beta_1\) på en lettfattelig måte
model <- lm(poeng~konsentrasjon, data=eksamendata)
summary(model)

Call:
lm(formula = poeng ~ konsentrasjon, data = eksamendata)

Residuals:
     Min       1Q   Median       3Q      Max 
-23.0078  -6.1458   0.0825   5.8221  23.8069 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    22.6031     3.0129   7.502 2.88e-11 ***
konsentrasjon   2.3258     0.2688   8.651 1.02e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.961 on 98 degrees of freedom
Multiple R-squared:  0.433, Adjusted R-squared:  0.4272 
F-statistic: 74.84 on 1 and 98 DF,  p-value: 1.015e-13

  1. Hva er forklaringskraften til modellen?

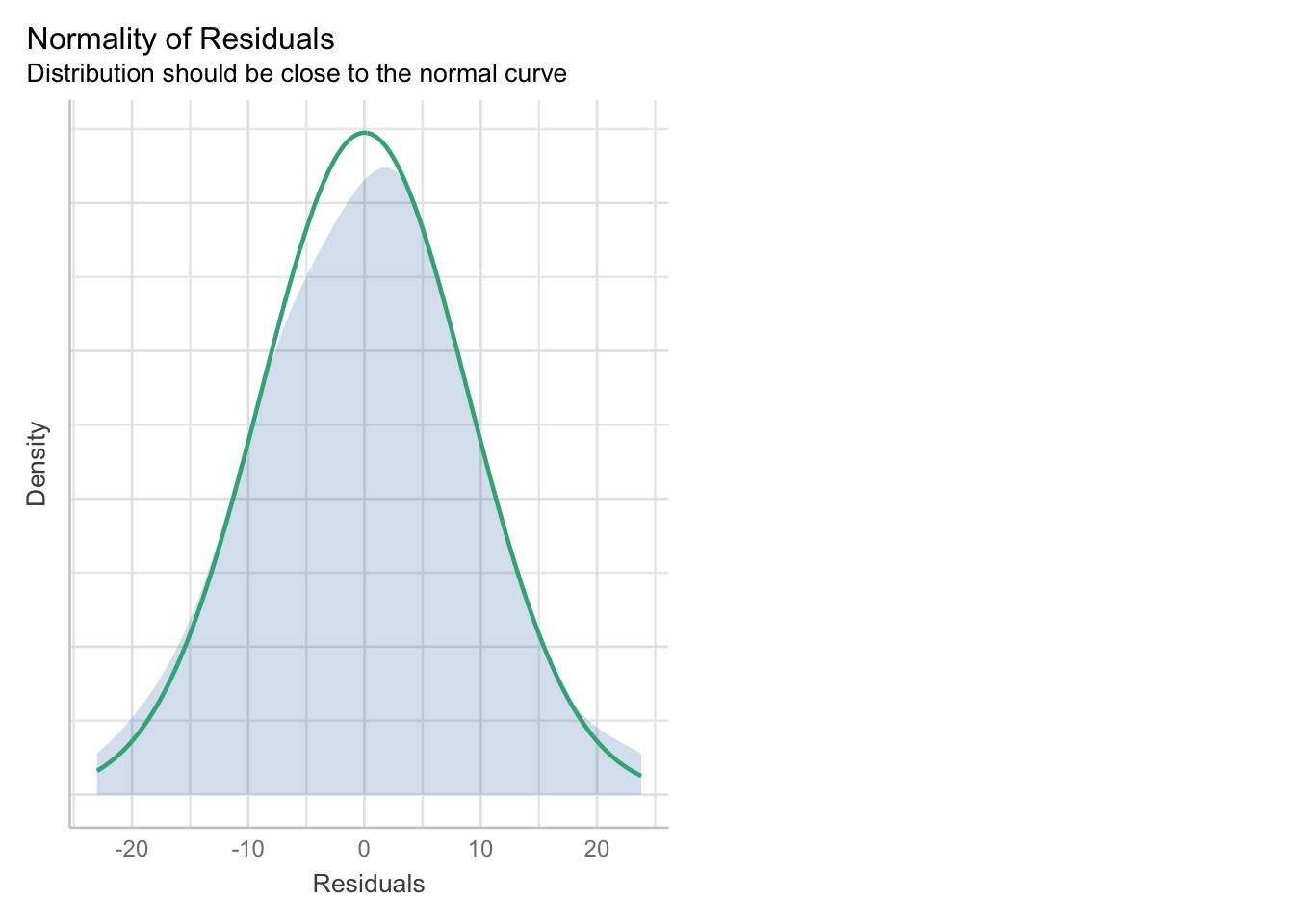
  2. Sjekk at de tre forutsetningene (linearitet, homoskedastisitet og normalitet av residualer) ser ut til å være oppfylt

library(performance)
check_model(model, check=c("linearity", "homogeneity", "normality"))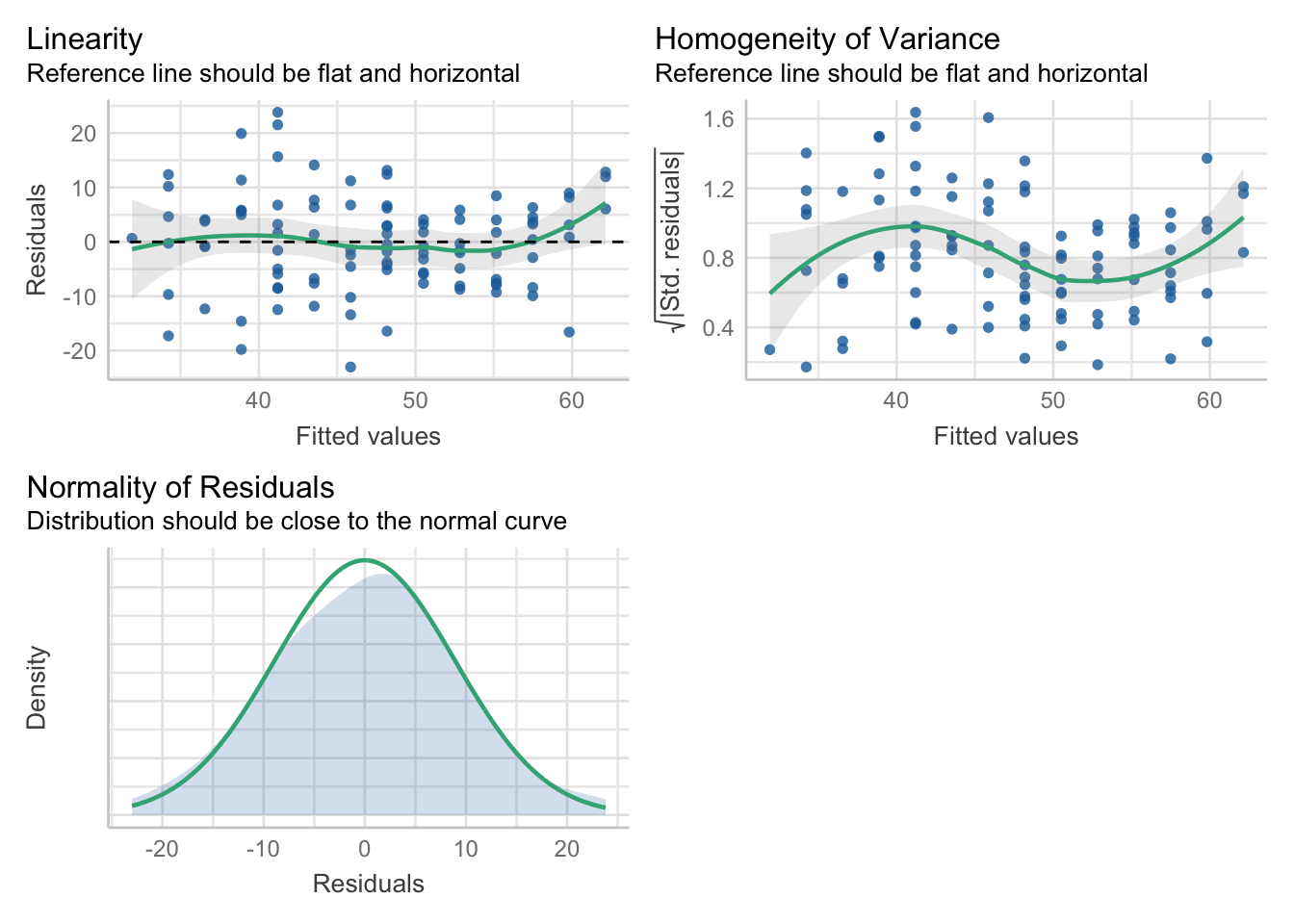

  1. Vi simulerer poengscore på ny, men nå med et ikke-normalt residual (khi-kvadrat fordelt)
set.seed(1)
poeng <- 25+2*konsentrasjon+rchisq(length(konsentrasjon), df=2)
eksamendata <- data.frame(poeng, konsentrasjon)

Kontroller at normalitetsantagelsen er brutt:

check_model(model, check=c("normality"))